아래 내용은 부스트코스 <자바로 구현하고 배우는 자료구조> 강의를 들으며 정리한 것입니다.
빅 오 표기법
어떤 알고리즘을 다른 알고리즘과 비교해서 표현할 때 사용하는 방법. 알고리즘의 효율성을 표시하는 표기법으로, 가장 많이 사용됨.
복잡도 n인 알고리즘에 빅 오 표기법 적용
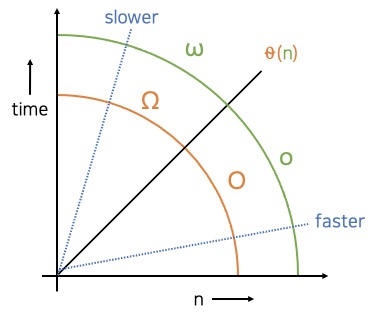
비교 대상이 되는 그래프가 어디에 위치하는 지에 따라, 이와 같이 표기하여 비교한다.
O (빅 오 복잡도) - same or faster. 같거나 더 빠름
θ (세타 복잡도) - same. 같음
Ω (빅 오메가 복잡도) - same or slower. 같거나 더 느림
o (리틀 오 복잡도) - faster (not same). 더 빠름
ω (리틀 오메가 복잡도) - lower (not same). 더 느림
생각해보기
1. 빅 오 표기법을 각각의 부등호에 대응하면 어떤 것인가?
| O | θ | Ω | o | ω |
| <= | < | >= | < | > |
2. 빅 오 표기법의 O는 무엇의 약자일까?
A: 뭔가 있을 것 같아 영어로 구글링 결과 'order of the function', 'order of'에서 유래했다고 한다. 직역하면 함수의 순서?
Big O notation is named after the term "order of the function", which refers to the growth of functions.
The big-O originally stands for "order of " ("Ordnung", Bachmann 1894), and is thus a Latin letter.
빅 오 표기법으로 알고리즘 비교
T/F 판단하기
문제1.
n^(4/3) = O(nlogn)
A. False.
풀이) 큰 수를 대입해본다. (계산기 사용) - 엄밀히 풀기 위해서는 로피탈 법칙을 사용해야 함
n = 1000이라고 할 때,
n^(4/3) = 10000, nlogn = 1000 log1000 = 3000
10000은 3000보다 훨씬 크므로, n^(4/3)은 O(nlogn)이 될 수 없다.
문제2.
3n³ + 4n² + 5n + 6 = θ(n³)
A. True
풀이)
비교 rule에 따라 상수와 낮은 차수를 무시하면 좌항의 식은 n³ 이 되므로, 세타(same)에 해당함
문제3.
n(n-1) / 2 = O(n²)
A. True
풀이)
좌항을 풀면 ½ n² - n, 상수와 낮은 차수 무시하면 n². 빅 오(same or faster)에 해당함
문제4.
2ⁿ = ω(n)
A. True
풀이) 큰 수를 대입해본다.
n = 1000이라면, 2^10 = 1024이므로 2^1000은 엄청 나게 큰 수. 2^n은 복잡도 n 기준 ω(slower)에 해당함(그래프 위쪽)
문제5.
n³ = O(n²)
A. False
풀이) n^3가 n^2보다 명백하게 크므로 O에 해당하지 않음
문제6.
n² = O(n³)
A. True
풀이) n^2가 n^3보다 작으므로 O에 해당함
생각해보기
Q. 문제 1에서 n=1을 대입하면 어떻게 되는가? 적당히 큰 수를 대입해야 하는 이유는 무엇인가?
A. n^(4/3) = O(nlogn)에서 좌항은 1, 우항은 0이 된다. 알고리즘 복잡도를 계산하고 비교하는 이유는 더욱 효율적으로 자료를 처리하기 위해서이므로, 항상 n이 무한대로 커질 경우를 가정하며 1 이하의 수는 거의 의미가 없다.
comment
위의 문제를 보며 알고리즘을 배우고 이해하는 것도, 프로그래밍도, 다른 어떤 것이든 이것을 왜 하며 어떤 의미가 있는지 그 본질을 우선시하는 것이 중요하다는 생각.
'Programming > java 자료구조' 카테고리의 다른 글
| 2-1) 연결 리스트, 노드와 크기 (0) | 2022.07.25 |
|---|---|
| 1-5) Autoboxing, 예외 처리 (0) | 2022.07.23 |
| 1-4) 제너릭 프로그래밍, 매개변수화 타입 (0) | 2022.07.23 |
| 1-3) 객체지향 프로그래밍, Comparable 인터페이스 (0) | 2022.07.23 |
| 1-1) 자료구조의 시작, 복잡성 (0) | 2022.07.20 |
